There are various evaluation measures and scores used to assess the performance of AI systems. As someone adopting a testing mindset in this context, those measures and scores are very important. Beyond simply understanding them as a concept, it’s important to see how they play out with working examples. That’s what I’ll attempt in this post.

The examples I’m going to focus on in this post are, arguably, simple to the point of being painfully simple. That means my examples are going to be illustrative rather than comprehensive. I’m doing this because I want to assume as little knowledge as possible.
Regarding the code examples I provide, they require nothing more than you copying and pasting them if you so wish. In fact, you don’t even have to execute them as I will attempt to explain what each is doing and how it relates to evaluation measures and scores.
Measures, Scores: What’s the Difference?
Let’s talk about the basic distinction between evaluation measures and scores first. They are often equated and that isn’t entirely wrong. There is a distinction but it can also be subtle.
 Evaluation measures are metrics or criteria used to assess the performance of AI systems. These measures provide a quantitative or qualitative indicator of how well the system is performing in a specific task or context. A key thing to keep in mind is that those specific tasks and contexts provide a localized interpretation — and thus contextual applicability — for the measures.
Scores are numerical values that represent the performance of an AI system according to a specific evaluation measure. That’s really how the two terms tie together. So, as an example, the “F1 score” is a commonly used score in classification tasks. This score combines precision and recall — two measures — into a single value.
Evaluation measures are metrics or criteria used to assess the performance of AI systems. These measures provide a quantitative or qualitative indicator of how well the system is performing in a specific task or context. A key thing to keep in mind is that those specific tasks and contexts provide a localized interpretation — and thus contextual applicability — for the measures.
Scores are numerical values that represent the performance of an AI system according to a specific evaluation measure. That’s really how the two terms tie together. So, as an example, the “F1 score” is a commonly used score in classification tasks. This score combines precision and recall — two measures — into a single value.
The basic idea is that measures and scores allow you to compare different AI systems or models based on their performance.
Performance of … What?
When we talk about the “performance” of an AI system in the context of evaluation and scoring, this typically refers to the system’s effectiveness and accuracy in accomplishing the task it was designed for. This is as opposed to the load or resource utilization of the architecture or infrastructure that the AI system is operating within.
So when we talk about “performance evaluation” in this context, this means we’re focusing on measuring how well the AI system performs in terms of achieving its intended goals or objectives, whatever those happen to be.

It’s very important to note that this kind of evaluation assesses the quality of the system’s outputs or predictions. In that context of assessing quality, this evaluation puts a lot of emphasis on the ability of the AI system to handle different scenarios or data variations.
That should sound a whole lot like what testers do with any software. Or even hardware, for that matter.
If you were to break down the idea of experiment-based testing into some of its most fundamental elements, you could say that it’s all about having one test condition that you apply a lot of data conditions to. Or, alternatively, it’s all about having one data condition that gets applied to various test conditions.
Performance Related to … What?
The evaluation and scoring of an AI system’s performance often involves comparing its outputs or results against “ground truth.” Here “ground truth” refers to human-labeled or human-annotated data. That data serves as a form of oracle, by which is meant an authoritative reference that helps us understand what “correct” looks like.

The evaluation measures and scores provide quantitative or qualitative assessments of the system’s performance relative to these oracles.
What About the Other Performance, Though?
The load or resource utilization of the system — such as CPU, memory usage, network bandwidth, or response time — falls under the scope of system performance or operational performance. These metrics are certainly important for assessing certain qualities of the AI system, such as efficiency, scalability, and reliability. But they are not directly related to the task-specific performance evaluation of the AI system.
So there’s a bit of a nomenclature distinction for you: task-specific performance and system performance.
Both aspects play a role in evaluating and optimizing AI systems. That said, it’s important to differentiate between them and focus on the appropriate metrics and measures depending on the specific evaluation goals and requirements that you’re dealing with.
This All Matters For Testing
When testing an AI system, evaluation measures and scores are absolutely essential tools to assess its performance and, ultimately, its effectiveness.
These measures provide objective and quantifiable ways to measure how well the AI system is accomplishing its intended goals and, more specifically, these measures help us make informed decisions about the AI system’s suitability for whatever its intended purpose is.
Suitability-to-purpose — sometimes called fitness-for-purpose — is an extremely important quality and not just in an AI context. This is a concept that specialist testers are very used to dealing with.
Put another way, these measures and scores help us focus on the outcomes and not just the outputs. That’s a distinction that no test specialist should have trouble accommodating.
Making informed decisions also means taking into account risks. And one of the key aspects of experiment-based testing is the ability to surface risks, particularly when those risks impact the suitability or fitness.
I bring all this up because it’s critical to me that testers see that AI systems are just another context in which to apply their specialist testing skills. I often see a bit too much fear around the idea that machine learning and artificial intelligence are somehow domains that require radically different styles of thinking and that’s not really true.
A Simple (But Practical) Example
You can feel free to follow along with this example, as well as any of the following code examples, if you have Python on your system. You would just need to make sure to use pip to install the various dependencies.
The two dependencies you’ll need right away are “numpy” and “scikit-learn”.
Even if you’re not entirely familiar with the code, take some time to look at it. One thing I find testers most often do not do in these contexts is critically analyze what they’re being asked to consider or execute. This is part of a wider problem I see in the test discipline — not just in the context of AI — where too many testers do not have adequate understanding of the underlying code.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
<p>import numpy as np <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p> |
In this example, I’m generating random binary classification data. This is a type of dataset where each data instance is assigned to one of two possible classes or categories. Here X refers to the input features and y refers to the binary labels.
You might notice that uppercase X but lowercase y and wonder about that. In the AI and machine learning context, it’s quite common to use uppercase variable names to represent feature data or input data matrices while lowercase variable names are often used for target variables or output vectors. If you’re a developer reading this, note that test specialists will notice and ask about things like this!
With the data generated, I then split the data into training and test sets using train_test_split. Then I train a logistic regression model using LogisticRegression. A “logistic regression” model is basically a statistical algorithm and it’s used to predict the probability of an instance belonging to a particular class based on a set of input features.
After the training is completed, I make predictions on the test set using the trained model.
All of what I just described is the core level mechanics of this example.

I’ll stress this point again: pay attention to the code, even if you don’t type it in or try to run it. Get a feel for the basic structure because the above basic structure, while being very simple, is indicative of how lot of machine learning projects are set up.
To evaluate the performance of the model in this example, I calculate an accuracy measure and the F1 score. Both of these use the true labels (y_test) and the predicted labels (y_pred) as input and compute the respective metrics.
The Meaning of Our Example Outputs
Okay, great. But what do those metrics actually mean?
If you asked that question, kudos to you because you are thinking like a tester. I bring this up because there’s actually a simple meaning to our measure (accuracy) but a more complex meaning to our score (F1).
Accuracy
The accuracy here measures the proportion of correctly predicted instances out of the total number of instances in the test set.
What that means is that the accuracy score represents the percentage of correct predictions made by the logistic regression model. A higher accuracy score indicates better overall performance because it shows how well the model correctly classified the binary labels in the test set.
F1 Score
The F1 score combines precision and recall measures to provide a balanced measure of the model’s performance.
What you’ll often hear that this means is that this score considers both the true positive rate (sensitivity) and the true negative rate (specificity).
However … that’s not entirely accurate. And recognizing that it’s not entirely accurate is an important skill for testers who are looking to judge what scores to use and how much to trust them.
I say the above is not entirely accurate because an F1 score doesn’t actually directly consider the true negative rate (specificity) in a binary classification task. Instead, the F1 score focuses on the balance between precision and recall, which are related to the true positive rate (sensitivity) and the false positive rate.
Let’s clarify some terminology.
- True Positive (TP) refers to instances that are correctly predicted as positive.
- False Positive (FP) refers to instances that are incorrectly predicted as positive.
- False Negative (FN) refers to instances that are incorrectly predicted as negative.
- True Negative (TN) refers to instances that are correctly predicted as negative.
As a tester in this context, I’ve very often seen people confuse and/or conflate the “true negative rate” with the “false positive rate” and that can lead to some problems.
Now let’s clarify how that terminology is used.
Precision is the ratio of true positives to the sum of true positives and false positives. In other words, it measures how many of the predicted positive instances are actually positive. Precision is calculated as TP / (TP + FP).
Recall (or sensitivity) is the ratio of true positives to the sum of true positives and false negatives. It measures how many of the actual positive instances are correctly identified. Recall is calculated as TP / (TP + FN).
The F1 score is the harmonic mean of precision and recall, providing a single metric that considers both precision and recall. The F1 score is calculated like this:
2 × (precision × recall) / (precision + recall)
For now, when I say “harmonic mean” just know that this type of mean emphasizes smaller values and provides a way to combine them into a single representative value. A way to think of it, perhaps, is that a harmonic mean gives more weight to smaller values. If the two numbers are close to each other, the harmonic mean will also be close to them. However, if one of the numbers is much smaller than the other, the harmonic mean will be pulled closer to the smaller value.
Whew. Okay, so what is all that telling us?
While sensitivity (true positive rate) is an essential component of the F1 score, specificity (true negative rate) is not directly incorporated. Specificity is often used in evaluating binary classifiers but it’s not part of the F1 score.
A higher F1 score indicates better precision and recall and that would demonstrate the model’s ability to accurately classify both positive and negative instances.
So this leads us to understand that what the F1 score actually means is a balance between two important aspects of a binary classification model’s performance: correctness and completeness.
We’re Starting to Interpret and Explain
What I’m taking you through above is a bit about two very important qualities we have to put front-and-center when working with AI systems: interpretability and explainability. These are ways to expose what’s really going on.

Let’s look at each in turn and use our example to illustrate the terms.
Interpretability
Precision, also known as positive predictive value, measures the correctness of the model’s predictions. It answers the question: “Of all the instances the model predicted as positive, how many were actually positive?” A high precision indicates that the model has a low rate of false positives, meaning it’s accurate in identifying positive instances. Recall, also known as sensitivity or true positive rate, measures the completeness of the model’s predictions. It answers the question: “Of all the actual positive instances, how many did the model correctly identify?” A high recall indicates that the model has a low rate of false negatives, meaning it can capture most of the positive instances.The F1 score we’re generating considers both precision and recall, finding a balance between correctness and completeness. The way I framed the questions above, with emphasis, probably shows how the terms are a bit intertwined.
The F1 score helps evaluate the overall effectiveness of the model by considering both false positives (incorrect predictions of positive instances) and false negatives (missed predictions of positive instances).
What this means is that the F1 score seeks to find the optimal tradeoff where precision and recall are maximized together. Thus a high F1 score indicates that the model has a good balance of correctly identifying positive instances (precision) and capturing a significant portion of all positive instances (recall).
Explainability
So we interpreted things. But now let’s explain them. By way of exmaple, let’s say we have a data set of 100 data points that need to be classified. Completeness (recall) refers to how well the model captures all the positive instances in the data set. In this case, it answers the question: “Of all the actual positive instances in the data set, how many did the model correctly identify?”
For our case, let’s say there are 20 positive instances in the data set. If the model correctly identifies 18 out of those 20 positives, then the recall (completeness) would be 18/20 or 90%. This would indicate that the model has a high recall, meaning it can capture a significant portion of the positive instances in the data set. Correctness (precision) refers to how well the model’s positive predictions align with the actual positive instances. It answers the question: “Of all the instances the model predicted as positive, how many were actually positive?”
In our case, if the model predicts 25 instances as positive, but only 18 of them are actually positive, then the precision (correctness) would be 18/25 or 72%. This indicates that the model has a lower precision, meaning there is a relatively higher rate of false positives.
With this added context for explaining our interpreted model, we can say that completeness (recall) measures how well the model captures all the positive instances in the data set, while correctness (precision) measures how well the model’s positive predictions align with the actual positive instances.
Responsible AI
I hope my reason for belaboring these points was clear: as a tester, you have to be very certain to understand what measures and scores you — or your delivery team — are considering. And you have to be certain that everyone is operating on an accurate distinction of what those measures and scores are actually capable of telling you.
This is a huge focus of responsible AI. Part of being “responsible” is that the AI system in question can be interpreted and explained.
Execute Our Model
If you run the example a few times and you’ll like see output like this:
Accuracy Measure: 0.55
F1 Score: 0.0
Accuracy Measure: 0.4
F1 Score: 0.45454545454545453
Accuracy Measure: 0.45
F1 Score: 0.3529411764705882
Accuracy Measure: 0.35
F1 Score: 0.48000000000000004
Accuracy Measure: 0.6
F1 Score: 0.5
The accuracy measure and F1 score can clearly vary between different runs of the program and this is due to the random generation of the binary classification data. The random initialization of the data and the random train-test split can result in different performance outcomes each time the model is executed.
What this means, crucially, is that the accuracy measure and F1 score are calculated based on the specific random data generated and the corresponding train-test split and, further, this randomness affects the model’s training and evaluation.
But as a tester you might be saying: “Well, if all is potentially varying, how do I reason about the model? Even with multiple data points, I’m only getting a single execution each time.”
And if you’re saying that, excellent! This means you’re thinking more about the ultimate outcome of the model rather than just the outputs from it. What you really want is confidence that the measure and score are accurately conveying the performance of the model.
So what do you do?
Who Tests the Tester?
The simple answer which you might have thought of is that you just perform multiple runs of the program and then average the evaluation metrics over those runs. On the other hand, if you have some experience in this arena, you instead might have thought of applying cross-validation techniques to assess the model’s performance a bit more comprehensively.
So let’s give both of those approaches a shot.
Cross-Validation
How would you apply a cross validation technique? The easiest way is that you can split the data into multiple subsets — which are called “folds” — and then perform training and evaluation on different combinations of these subsets. Once that’s done you can then return the evaluation metric for each fold. Here’s an updated version of the example that incorporates cross-validation.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
<p>import numpy as np <p>from sklearn.model_selection import cross_val_score <p>from sklearn.linear_model import LogisticRegression <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>model = LogisticRegression() <p>scores = cross_val_score(model, X, y, cv=5, scoring="accuracy") <p>avg_accuracy = np.mean(scores) <p>f1_scores = cross_val_score(model, X, y, cv=5, scoring="f1") <p>avg_f1 = np.mean(f1_scores) <p>print("Accuracy Measure (average):", avg_accuracy) <p>print("F1 Score (average):", avg_f1) <p> |
Here you’ll notice that I’m not using the train_test_split anymore. Instead, the cross_val_score function is used to perform what’s called a 5-fold cross-validation. That’s what the cv=5 is specifying.
There’s a technical description for this but what it boils down to is that I’m splitting the data into five subsets (folds), training the logistic regression model on four of those folds, and evaluating the performance on the remaining fifth fold.
That process is then repeated for each fold which results in five evaluation metrics for both the accuracy measure and the F1 score. The average accuracy measure and average F1 score are calculated by taking the mean of the respective metrics obtained from the cross-validation.
Execute Our Model
If you execute this cross-validated model a few times, you’ll see output like this:
Accuracy Measure (average): 0.6100000000000001
F1 Score (average): 0.7575757575757576
Accuracy Measure (average): 0.47000000000000003
F1 Score (average): 0.6208966087675766
Accuracy Measure (average): 0.53
F1 Score (average): 0.5318713450292398
Accuracy Measure (average): 0.54
F1 Score (average): 0.44494569757727653
Accuracy Measure (average): 0.5900000000000001
F1 Score (average): 0.0
Uh, wait … is that better? This looks like my previous execution run. Well, output-wise it is, but keep in mind what the model is doing differently.
By applying cross-validation, you obtain a more reliable estimate of the model’s performance by evaluating it on different subsets of the data. This helps to assess the model’s generalization ability and provides a more vigorous evaluation of its performance compared to the single train-test split I was doing previously.
But this is showcasing a crucial point. As a tester, if you are just given both sets of outputs you would really have no idea that they came from different ways of executing the model. So the observability part here is crucial: you have to understand how the outputs are generated.
Multiple Runs
I mentioned that another way to do this instead of cross-validation would be to perform multiple runs of the program, averaging the evaluation metrics over those runs. Let’s take a look at how to do this. Conceptually, it’s pretty easy: just throw the brunt of the program in a loop and store the evaluation metrics for each run.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
<p>import numpy as np <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>num_runs = 5 <p>accuracy_measures = [] <p>f1_scores = [] <p>for run in range(num_runs): <p> X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=run <p> ) <p> <p> model = LogisticRegression() <p> model.fit(X_train, y_train) <p> <p> y_pred = model.predict(X_test) <p> <p> accuracy = accuracy_score(y_test, y_pred) <p> f1 = f1_score(y_test, y_pred) <p> <p> accuracy_measures.append(accuracy) <p> f1_scores.append(f1) <p>avg_accuracy = np.mean(accuracy_measures) <p>avg_f1 = np.mean(f1_scores) <p>print("Accuracy Measure (average):", avg_accuracy) <p>print("F1 Score (average):", avg_f1) <p> |
Here the program executes the loop num_runs times, each time randomly splitting the data into training and test sets using a different random seed. That’s what the random_state=run part is doing.
For each run, the logistic regression model is trained, predictions are made on the test set, and evaluation metrics are calculated. After completing all the runs, the average accuracy and average F1 score are calculated by taking the mean of the respective scores stored in the lists.
Why Choose? I’ll Use Both!
Even if you don’t have the full mathematical context of all this, let me ask you this: would you recommend combining both the multiple runs as well as the cross-validation?

I see this come up a lot with testers who are shown various techniques for getting better reliability and there seems to be this pull towards incorporating all of them. This is often under the assumption that if each is good on its own, together they would get even more reliability. But is that correct?
In our context here, no. Including both multiple runs and cross-validation in the same evaluation process isn’t necessary and, in fact, wouldn’t be in most cases.
- Multiple runs with train-test splits help capture the variability in performance that can arise from different random splits of the data. By averaging the evaluation scores over multiple runs, you can obtain a more robust estimate of the model’s performance.
- On the other hand, cross-validation provides a more comprehensive evaluation by systematically splitting the data into multiple folds and performing training and evaluation on different combinations of these folds. It helps assess the model’s generalization ability and stability across different subsets of the data.
Put another way, both approaches serve a similar purpose of assessing the model’s performance and obtaining more reliable estimates, but they achieve it in different ways. Using both approaches together, far from helping, can actually be harmful (in terms of computational overhead) or obfuscating (in terms of redundant evaluations).
So what’s the lesson here?
Mainly that it’s advisable to choose one approach based on the available resources, time constraints, and specific requirements of your evaluation. This means it’s all heuristic-based.
If you have sufficient data and computational resources, cross-validation is often a preferred choice because it provides a more thorough evaluation. However, if data is limited, multiple runs with train-test splits can still provide valuable insights into the model’s performance.
Which heuristics you apply will, of course, be very context-dependent. And context-dependent heuristics are something test specialists deal with all the time.
Visualize to Understand
Let’s look at another really important way to better understand your model and what the outputs of your model are. This is by visualizing the numeric outputs. Let’s use the original “train/test split” example but include a visualization component to it.
This code uses “matplotlib” library to create a scatter plot so you’ll need to install that dependency.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
<p>import numpy as np <p>import matplotlib.pyplot as plt <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>plt.scatter( <p> X_test[:, 0], X_test[:, 1], c=y_test, cmap="bwr", label="Actual", marker="s" <p>) <p>plt.scatter( <p> X_test[:, 0], <p> X_test[:, 1], <p> c=y_pred, <p> cmap="bwr", <p> label="Predicted", <p> edgecolors="black", <p> linewidths=1, <p> marker="o", <p>) <p>plt.xlabel("Feature 1") <p>plt.ylabel("Feature 2") <p>plt.title("Binary Classification Results") <p>plt.legend() <p>plt.show() <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p> |
You should see something like this.

Now, from a test specialist standpoint, what is that scatter plot actually telling you? What would you be telling someone to look for in that visual in order to interpret it if these were your test results?
The visualization with overlapping red and blue data points suggests that the model’s predictions align with the actual labels, indicating correct predictions. The overlapping data points represent instances where the model correctly classified the samples.
Don’t Confuse Quantitative with Qualitative!
It’s important to note that the accuracy of the model cannot be determined solely based on the overlapping points in the visualization. The accuracy measure and F1 score generated as part of the output actually provide more reliable quantitative measures of the model’s overall performance. That is really important — but do you see why?
Ask yourself this: is it accurate to say that the actual plot points are not the F1 scores and accuracy measure?
Answer: yes, that is accurate to say. The plot points in the visualization represent the actual class labels (y_test), while the predicted plot points represent the predicted class labels (y_pred) generated by the model. The F1 score and accuracy measure, on the other hand, are quantitative metrics that assess the overall performance of the model based on the predicted and actual labels. The visual representation of the data points helps us visually inspect the distribution and overlap of the predicted and actual labels in the feature space. However, it does not directly convey the F1 score or accuracy measure.
While the visual representation can be helpful to gain a qualitative understanding of the model’s predictions, it must be complemented with the numerical evaluation metrics to assess the model’s accuracy comprehensively. This is an extremely crucial point to keep in mind!
Many Ways to Visualize
Let’s consider another way to visualize.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
<p>import numpy as np <p>import matplotlib.pyplot as plt <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>xx, yy = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100)) <p>Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) <p>Z = Z.reshape(xx.shape) <p>plt.contourf(xx, yy, Z, alpha=0.8, cmap="bwr") <p>plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap="bwr", label="Actual") <p>cbar = plt.colorbar() <p>cbar.set_label("Predicted") <p>plt.xlabel("Feature 1") <p>plt.ylabel("Feature 2") <p>plt.title("Binary Classification Results (Decision Boundary)") <p>plt.legend() <p>plt.show() <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p> |
This provides a decision boundary plot. What this does is show the boundary or the region where the model predicts one class or the other. This can give you a visual representation of how the model separates the data points based on their features. You’ll likely get something like this:

But … how would you explain that? As a tester, just looking at that visual, what do you think might be missing?
You might be thinking: “Should the legend include Actual and Predicted?” And that’s a great question. But even more fundamentally you might ask: “What’s the actual decision boundary there? If these are my test results, I don’t know that I see a clear pass/fail concept.”
In fact, those two questions are a bit related. Regarding the first question, what a data scientist might tell you is that the legend currently includes the label “Actual” for the scatter plot. Since the decision boundary is being plotted separately, it’s not necessary to include “Predicted” in the legend since it represents the decision boundary rather than the individual predicted points. But, as a tester who wants more explainability, that leads us right back to our second question: where actually is that boundary? Here’s what I would advocate for instead.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
<p>import numpy as np <p>import matplotlib.pyplot as plt <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>xx, yy = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100)) <p>Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) <p>Z = Z.reshape(xx.shape) <p>plt.contourf(xx, yy, Z, alpha=0.8, cmap="bwr") <p>plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap="bwr", label="Actual") <p>cbar = plt.colorbar() <p>cbar.set_label("Predicted") <p>plt.xlabel("Feature 1") <p>plt.ylabel("Feature 2") <p>plt.title("Binary Classification Results (Decision Boundary)") <p>plt.legend() <p>plt.show() <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p> |
You’ll get something like this:

Here the colorbar on the provides a visual representation of the predicted classes corresponding to the decision boundary.
But how do we explain the visual?
The fully red background represents the region where the model predicts the positive class (class 1), while the fully blue background represents the region where the model predicts the negative class (class 0). The line separating the two background areas represents the decision boundary that the model has learned.
This visualization suggests that the model has identified a clear boundary between the two classes based on the input features. Instances falling on one side of the boundary are predicted as one class, while instances falling on the other side are predicted as the other class. The decision boundary helps to visually understand how the model is separating the input space to make predictions.
This can differ quite a bit between executions:

Seeing how the decision boundary shifts under varying conditions of the model execution can tell you much about its prediction stability.
Test Analysis
In the above examples, by examining the scatter plot, considering the actual and predicted labels, and looking at the decision boundaries, you can help the delivery team gain insights into how well the logistic regression model performs in separating the two classes and correctly classifying the test instances. This is what helps the team understand the model’s behavior and, by doing so, evaluate its effectiveness for this particular task.
Let’s consider one more visualization.
You will need the “seaborn” library for this.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
<p>import numpy as np <p>import seaborn as sns <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>from sklearn.metrics import confusion_matrix <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>cm = confusion_matrix(y_test, y_pred) <p>sns.heatmap(cm, annot=True, cmap="Blues") <p>plt.xlabel("Predicted labels") <p>plt.ylabel("True labels") <p>plt.title("Confusion Matrix") <p>plt.show() <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p> |
This is a confusion matrix plot. This kind of plot provides a visual representation of the performance of a classification model by showing the counts or percentages of true positives, true negatives, false positives, and false negatives. It can be useful to evaluate the model’s performance in terms of different types of errors it makes or how confused it seems to be, if you prefer. You might see something like this:

In the confusion matrix visual, the rows represent the true labels, and the columns represent the predicted labels. The numbers within the matrix indicate the counts of instances falling into each category.
- The top-left cell with the value 9 represents the number of instances that are actually labeled as 0 (true label) and correctly predicted as 0 (predicted label). These are called true negatives.
- The top-right cell with the value 0 represents the number of instances that are actually labeled as 0 (true label) but incorrectly predicted as 1 (predicted label). These are called false positives.
- The bottom-left cell with the value 11 represents the number of instances that are actually labeled as 1 (true label) but incorrectly predicted as 0 (predicted label). These are called false negatives.
- The bottom-right cell with the value 0 represents the number of instances that are actually labeled as 1 (true label) but incorrectly predicted as 1 (predicted label). These are called true positives.
So what the confusion matrix is doing here is providing a visual summary of the model’s performance in terms of correctly and incorrectly classified instances for each class. It helps in evaluating the model’s accuracy and understanding the types of errors it makes.
In the case of the above output, the model has correctly classified 9 instances as 0 and 0 instances as 1. However, it has incorrectly classified 11 instances as 0 when they are actually 1. The model has not predicted any instances as 1.
Let’s consider output from another model execution.

This time the model correctly classified 7 instances as 0 and 6 instances as 1. It incorrectly classified 2 instances as 1 when they were actually 0, and 5 instances as 0 when they were actually 1.
From a testing standpoint, with everything I just described, hopefully you can see the test and data conditions. Your goal, as a test specialist, is to expose those test and data conditions to others so that they can understand how everything worked to produce the outputs it did. That, in turn, helps determine if the ultimate outcome is being achieved.
With the above examples, we have enough data to allow us to actually perform test analysis because we can identify patterns of misclassifications and assess the model’s overall accuracy while also using quantitative accuracy measures and F1 scores to assess the model’s overall performance.
Explaining and Interpreting (Again)
That idea of determining if the ultimate outcome is being achieved is a key part of what is probably the most important quality we deal with in the testing industry: trust.
An application, whether AI-based or not, must be trusted by its users. If your application erodes confidence then it also compromises trust.
In order to help us understand how much we should or shouldn’t trust our AI systems, in particular, those qualities of explainability and interpretability are very important, which is why I’m revisiting them once again.
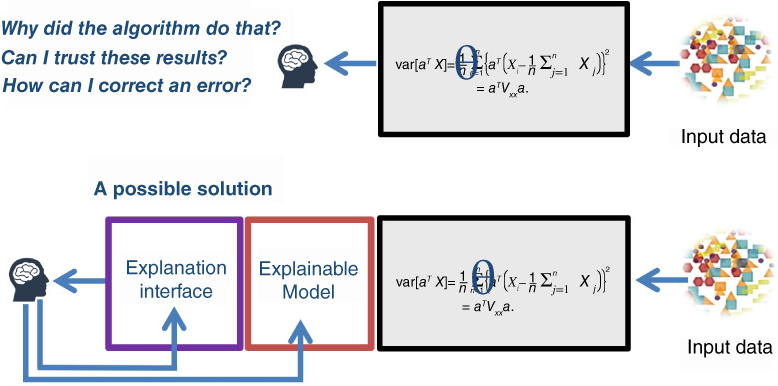
These qualities are often provided for via certain methods. This is a huge topic but let’s jump a little into the deep end of the pool and consider two of those methods.
Methods for Explaining and Interpreting
LIME (Local Interpretable Model-agnostic Explanations) and SHAP (SHapley Additive exPlanations) are two very popular methods for interpreting and explaining the predictions or outputs of machine learning models in the context of AI systems. These methods help provide insights into the decision-making process of these models and those insights thus enhance the transparency of the models.Transparent decision-making sounds like a good way to approach trustability, right?
Now, those methods sound complicated, don’t they? Well, let’s break them down a little and I’ll think you’ll see they’re not all that bad.
LIME
You’ll hear LIME described as a technique used to explain individual predictions made by complex machine learning models. That’s true, as far as it goes. But a more complete way to explain it is that LIME provides local, interpretable explanations by approximating the behavior of the underlying model around a specific data point.
“Local” here has a very specific meaning. It means specific to individual instances or data points rather than being global or general explanations that apply to the entire dataset or model. Think of it as “explanations being tailored to individual instances” rather than “explanations that are highly generalized to many instances.”
Most test specialists have heard of mutation testing. Well, there’s something similar lurking here. LIME achieves what I just described by perturbing the features of the input data point and observing how the model’s predictions change.
By examining the local changes in predictions, LIME generates explanations that highlight the features most influential in the model’s decision for that specific instance. LIME is considered “model-agnostic” because it can be applied to various types of models without requiring knowledge of their internal workings.
SHAP
That last point is similar to SHAP. SHAP is also considered “model-agnostic” in its ability to handle a wide range of models, thus not assuming any specific model architecture or training method. SHAP is based on the concept of Shapley values which is a concept taken from cooperative game theory. What does that actually mean, though?
Well, imagine this: you have a group of co-workers who want to divide an office reward among themselves fairly based on their contributions. Shapley values are a way to measure the importance or value of each person’s individual contribution to the group.
To determine each person’s Shapley value, you would consider all possible combinations of people in the group and calculate how much each persons adds to the group’s overall value when joining or leaving different combinations. The Shapley value is the average contribution of each person across all possible combinations.
So, broadly speaking, SHAP assigns values to each feature of an input data point by quantifying their contribution to the difference between the model’s prediction and a reference prediction. There’s a lot of detail to that but the summary view is that SHAP provides a holistic explanation by considering all possible feature combinations and calculating their contributions using Shapley values. This approach helps to work towards fairness and consistency in attributing the importance of each feature to the model’s prediction.
Above you saw me say “feature” a few times. In this context, a “feature” refers to an individual measurable property or characteristic of a data point or input. Put another way, a feature represents a specific aspect or attribute of the data that’s considered relevant or informative for making predictions or performing some task.

The key takeaway here is that these methods help improve the interpretability and explainability — and thus the transparency — of these models. Each of those things are types of quality.
This is important because the number one enemy of quality is opacity. Thus interpretability and explainability methods help us better understand the factors influencing the model’s decisions and — crucially — addressing ethical concerns related to fairness, bias, and accountability.
It’s only by being able to to interpret and explain that you have any chance of aligning all of this stuff with any notion of ethics. Because of that, I can’t stress enough the importance of understanding these kinds of concepts. Let’s explore these ideas in the context of our running example.
Using LIME
First, we’ll reframe our example using LIME. To do this, the general strategy is you have to select a specific instance from the test set for which you want to generate an explanation. Then you need to prepare the instance in a suitable format for LIME. In this case, you would need to convert the instance to a tabular representation, where each feature corresponds to a column.
Once you’ve done that, you use LIME to generate explanations for that instance. LIME works by creating what are called “local surrogate models” around the instance and approximating the model’s behavior in that locality. It perturbs the instance by sampling nearby instances and observes how the model’s predictions change.
The resulting explanations highlight the important features contributing to the model’s decision for that instance. So let’s add some code and try this out.
Make sure you have the “lime” library installed before running this code.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
<p>import numpy as np <p>from lime import lime_tabular <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p>instance_index = 0 <p>instance = X_test[instance_index] <p>feature_names = ["Feature 1", "Feature 2"] <p>class_names = ["Class 0", "Class 1"] <p>explainer = lime_tabular.LimeTabularExplainer( <p> X_train, feature_names=feature_names, class_names=class_names <p>) <p>explanation = explainer.explain_instance( <p> instance, model.predict_proba, num_features=len(feature_names) <p>) <p>explanation.save_to_file("classify_explanation.html") <p> |
After running this code, the LIME explanation will be saved to a file named “classify_explanation.html” in the current directory with your script.
You’ll see something like this:

But what does that mean?
The “Prediction probabilities” are shown as 0.49 for Class 0 and 0.51 for Class 1. These probabilities indicate the model’s confidence in each class prediction. Let’s break down the other parts.
- The LIME explanation for Class 0 states that when “Feature 1” is greater than 0.81, it contributes towards the model predicting Class 0. This suggests that values of “Feature 1” above 0.81 are indicative of Class 0.
- The LIME explanation for Class 1 states that when “Feature 2” falls within the range of 0.32 to 0.53, it contributes towards the model predicting Class 1. This suggests that values of “Feature 2” within this range are indicative of Class 1.
The LIME explanation provides insights into how the model makes predictions for individual instances by highlighting the important features and their contribution to the predicted class. In this case, the explanation suggests that “Feature 1” values above 0.81 favor Class 0 predictions, while “Feature 2” values within the range of 0.32 to 0.53 favor Class 1 predictions.
But again keep in mind the important caveat: LIME provides local, interpretable explanations specific to the given instance, aiming to shed light on the model’s decision-making process for that particular case.
For completeness, let’s also consider the same example with SHAP.
You will need to get the “shap” library to run the code.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
<p>import numpy as np <p>import shap <p>from sklearn.model_selection import train_test_split <p>from sklearn.linear_model import LogisticRegression <p>from sklearn.metrics import accuracy_score, f1_score <p>X = np.random.rand(100, 2) <p>y = np.random.randint(0, 2, 100) <p>X_train, X_test, y_train, y_test = train_test_split( <p> X, y, test_size=0.2, random_state=42 <p>) <p>model = LogisticRegression() <p>model.fit(X_train, y_train) <p>y_pred = model.predict(X_test) <p>accuracy = accuracy_score(y_test, y_pred) <p>f1 = f1_score(y_test, y_pred) <p>print("Accuracy Measure:", accuracy) <p>print("F1 Score:", f1) <p>instance_index = 0 <p>instance = X_test[instance_index] <p>explainer = shap.KernelExplainer(model.predict_proba, X_train) <p>shap_values = explainer.shap_values(instance) <p>force_plot = shap.force_plot( <p> explainer.expected_value[1], <p> shap_values[1], <p> instance, <p> feature_names=["Feature 1", "Feature 2"], <p>) <p>shap.save_html("classify_explanation.html", force_plot) <p> |
After running this code, just like before, the SHAP explanation will be saved to a file named “classify_explanation.html” in the current directory with your script.
You’ll see something like this:

Great. But how do we explain it?
In a SHAP force plot, the “higher lower” section at the top represents the predicted probability for the positive class. In our case, the predicted probability ranges from approximately 0.4375 to 0.4875, with 0.45 being bolded. This range indicates the model’s uncertainty in predicting the positive class for the instance being explained.
The line at the 0.45 mark separates the “higher” and “lower” sections, indicating the side of the line where the prediction is higher or lower than the base value. The base value represents the expected output of the model for an average prediction. The value of 0.45 being bolded suggests that the model’s prediction for the instance lies closer to that threshold.
On the left side of the line, where it says “Feature 1 = 0.8689,” it means that the contribution of Feature 1 is positive, pushing the prediction higher than the base value. The value of 0.8689 represents the value of Feature 1 for the instance being explained.
On the right side of the line, where it says “Feature 2 = 0.8002,” it means that the contribution of Feature 2 is negative, pulling the prediction lower than the base value. The value of 0.8002 represents the value of Feature 2 for the instance being explained.
These contributions indicate how each feature influences the model’s prediction. Positive contributions push the prediction higher, while negative contributions pull it lower. The magnitude of the contributions reflects the importance of each feature.
By analyzing the SHAP force plot, you can gain insights into how individual features contribute to the model’s prediction for a specific instance. It helps you understand which features have a positive or negative impact and the relative importance of each feature in determining the outcome.
A Simplified Deep Dive
Wait, is “simplified deep dive” an oxymoron? Hmm, I’m not sure but I feel like that’s what we did in this post. I hope you got a feel for how the testing mindset and skillset plays out in the context of an example.
While the example here was extremely small, using entirely anonymously generated random data, that example — serving as the basis for a binary classification task — is very real and operative in many industries. It’s found in medical diagonstics in healthcare, credit score modeling in financial institutions, customer segmentation in marketing, spam detection in email service providers, fraud and anomaly detection in various industries and so on.
What I hope you saw is that the ability to interpret and explain is crucial. And one of the keys to being able to interpret and explain is to have a focus on testability, which means observability and controllability at minimum.
In the second part of this post, I’ll cover a few more examples but also bring in a few more testing ideas. That post will also focus a bit on the ethics that need to be front-and-center for this kind of investigation.