Many are debating the efficacy of artificial intelligence as it relates to the practice and craft of testing. Perhaps not surprisingly, the loudest voices tend to be the ones who have the least experience with the technology beyond just playing around with ChatGPT here and there and making broad pronouncements, both for and against. We need to truly start thinking about AI critically and not just reacting to it if we want those with a quality and test specialty to have relevance in this context.

This series does have a bit of an introduction in terms of its rationale. See the posts Computing and Crucible Eras and Keeping People in Computing if you’re curious. That said, those two posts are not required reading at all for this series.

Getting Through the Barrier

Soumith Chintala, the co-creator of the PyTorch framework, made a good point about the challenge of learning artificial intelligence when he said “you slowly feel yourself getting closer to a giant barrier.” Soumith further says:

This is when you wish you had a mentor or a friend that you could talk to. Someone who was in your shoes before, who knows the tooling and the math — someone who could guide you through the best research, state-of-the-art techniques, and advanced engineering, and make it comically simple.

Yes, entirely, I agree. That’s part of what my blog posts are attempting to be. I would hesitate to say mentor when applied to me but I would not hesitate at all to say friend and hesitate even less to say I’ve likely been in the same shoes. I too reached that barrier that Soumith talks about and struggled mightily with it. I still do. My entire machine learning series was all about that struggle. The same, in some ways, applied to my more limited data science series. My AI Testing series was me finally finding some confidence to speak more broadly.

I’m not sure which author — Jeremy Howard or Sylvain Gugger — specifically had the thought but in their book Deep Learning for Coders with fastai and PyTorch: AI Applications Without a PhD, one of them states the following:

The hardest part of deep learning is artisanal: how do you know if you’ve got enough data, whether it is in the right format, if your model is training properly, and, if it’s not, what you should do about it? That is why we believe in learning by doing. … The key is to just code and try to solve problems: the theory can come later, when you have context and motivation.

Theory later as context and motivation kick in. That was a key element for me that I had to realize early but had not articulated. Yet there’s a healthy balance here. There’s an interplay of theory and practice that I find is needed. The problem I found is that a lot of the resources out there were of two broad types.

• I found some resources were highly conceptual and mathematical. These gave me extensive mathematical explanations of what was going on so I could “understand the theory.”
• I found other resources that had intricate blocks of code. And if I could figure out how to run that code, this would apparently show me what was going on so I could “understand the practice.”

What I often came away with was understanding neither to any great extent. Hence by above-mentioned blogging. It was my way to make myself understand. I wrote those posts as if I was my audience. I figured if I couldn’t write it, I probably didn’t understand it.

Leveraging Mental Models

Seth Weidman, in his book Deep Learning from Scratch: Building with Python from First Principles, said the following:

With neural networks, I’ve found the most challenging part is conveying the correct ‘mental model’ for what a neural network is, especially since understanding neural networks fully requires not just one but several mental models, all of which illuminate different (but still essential) aspects of how neural networks work.

I entirely agree with that. What’s often not stated is what the mental models actually are. I would say they are the following:

• Mathematical and statistical reasoning
• Visualizing and graph notations
• Abstraction and generalization
• Pattern recognition
• Experimentation and iteration
• Systems thinking
• Creativity and intuition

I would actually argue that these are skills that quality and test specialists should already have anyway.

Going back to Weidman for a second, he mentions that each of these three statements is a valid way of looking a neural networks:

• A neural network is a mathematical function that takes in inputs and produces outputs.
• A neural network is a computational graph through which multidimensional arrays flow.
• A neural network is a universal function approximator that can in theory represent the solution to any supervised learning problem.

But what do those statements actually mean?

Well, I’m going to give one way of looking at those statements in this post. Yet here’s the problem: you have to implement the ideas to be able to actually understand them. There’s the practice part. Yet, to understand your implementation, you have to focus on why the implementation conceptually makes sense. That’s the theory part. That’s what posts in my “Thinking About AI” series are going to do: focus on implementation so that practice and theory follow.

One book I greatly enjoyed was by David Perkins called Make Learning Whole: How Seven Principles of Teaching Can Transform Education. In his book Perkins talks about the idea of “play the whole game.” Of that, Perkins says:

We can ask ourselves when we begin to learn anything, do we engage some accessible version of the whole game early and often? When we do, we get what might be called a ‘threshold experience,’ a learning experience that gets us past initial disorientation and into the game.

This idea of threshold experiences resonates with me quite deeply. As someone with intense — and deserved — imposter syndrome through much of my life, I’ve had to find and foster these threshold experiences as much as I can. The challenge is that they aren’t given to you. You have to create them in some ways. But other people can help to enable that creation.

That’s what I’m hoping my various musings on artificial intelligence will do for people who learn the same way I do.

Let’s Get Our Concepts In Place

At it’s core, programming is about what? Well, it’s pretty simple if you get reductionist enough. It’s about having some inputs, sending those inputs to a program, and then having that program generate some outputs or results.

From a purely black box perspective, we can consider the program itself to be one big function. This notion of a function is important conceptually but it’s also really simple. Consider this function:

f₁(x) = x²

This is a function represented in mathematical notation. It’s called a square function. You could also represent this function as a graph.

This is just a parabola that opens upwards. But we can also represent a function as a black box that takes in inputs and generates outputs.

Here we have the generic schematic of the function at the top with some examples of it in use. We pretty much just described conceptually how machine learning works. Why? Broadly, what all this means is that programs are essentially working on a given task using data. Now consider that machine learning has, as its basis, a lot of programming. Similar to programming, the basis of machine learning is essentially that of learning representations suitable for a task from data. That learning is done by a function.

A difference here is that in traditional programming, the program’s logic is explicitly defined by the programmer. In contrast, in machine learning, the program learns from data to make predictions or decisions without being explicitly programmed for every task. This key difference makes machine learning a powerful approach for tasks like pattern recognition, decision-making, and prediction in situations where explicit programming may be challenging or not feasible.

And, earlier, when I said “learning representations suitable for a task”, think of it as a program having to discern different visual features of objects, such as edges, textures, and shapes, in a way that enables it to distinguish between different classes of objects. Or think of it as a program having to discern semantic relationships and similarities between words and sentences to distinguish various sentiments or attitudes.

One aspect of machine learning is called deep learning.

Deep learning, when you boil away all the details, is fundamentally simple. It’s nothing more or less than a technique to extract and transform data. All of deep learning is based on a single type of model called the neural network. And this neural network can be thought of as a program!

Notice how this is the exact same visual I showed you earlier but with a word replacement.

Specifically, the model is a program that contains an algorithm. Think of it as a big old function! And this function is a mathematical and computational representation that’s been designed to mimic the behavior of the human brain’s neural network. This model &mdash this program — takes data as input and produces results.

The extraction and transformation of data that I mentioned is done by using multiple layers of neural networks.

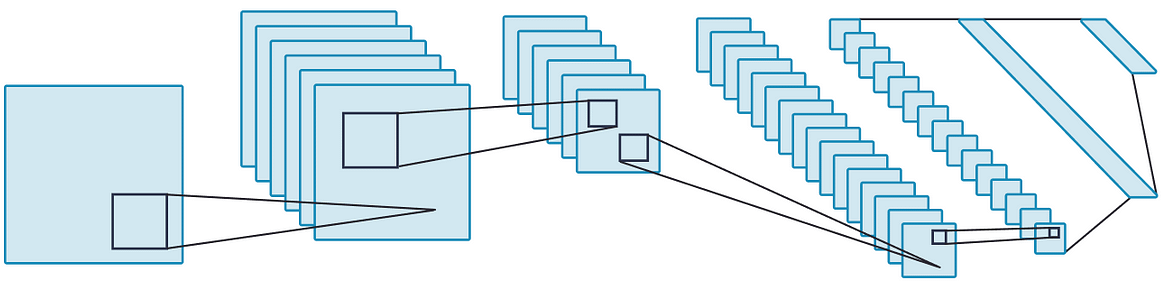
Maybe think of these layers is individual functions being called by the one main function. Each of these layers takes its inputs from previous layers and progressively refines them. A key conceptual point here is that these layers are trained by algorithms that are designed to minimize their errors and thus improve their accuracy.

In this way, a neural network learns to perform a specified task.

The Concepts Are Fundamentally Simple

So the main thing to get here is that a neural network is a particular kind of machine learning model that is mathematical in nature and inspired by how neurons in the human brain seem to work. Deep learning is a technique that utilizes neural networks to extract and transform data. Each of layers that make up a neural network layers take inputs from previous layers and progressively refine those inputs. Through a process of training, algorithms minimize errors and improve accuracy, allowing the network to learn and get better at performing a specified task.

All coding you do to learn the above will be an implementation of what I just said there. Yes, there can be a lot of details. But all of those details essentially converge to the above statement.

Okay, so that’s coding. But what about the testing? Well, obviously, where there’s code, there can be testing of that code. But here’s an interesting thing: these models have a built-in way to determine some aspects of their quality. You can test if the errors are actually being minimized and if the accuracy is actually improving.

Using Models For Tasks

I’ve mentioned tasks a few times so let’s get a little more specific on that. One of the tasks might be natural language processing and it’s one of the tasks I’m going to be looking at first in this series.

Broadly speaking, natural language processing refers to a set of techniques that involve the application of statistical methods, with or without insights from the study of linguistic, to understand text in order to deal with real-world tasks. When I say “with or without insights from the study of linguistics” this means that natural language processing techniques can be developed either purely based on statistical methods and machine learning algorithms or by incorporating linguistic principles to enhance language understanding.

This “understanding” of text — whether statistical, linguistic or both — is derived by transforming texts to useable computational representations. These representations are discrete or continuous combinatorial structures framed as mathematical objects. A combinatorial structure here just refers to a mathematical arrangement or configuration of elements. When I say “mathematical arrangement,” this means like vectors, matrices, tensors, graphs, and trees. These structures are used to represent and analyze relationships or patterns in data.

Deep learning enables you to create models — programs — that efficiently learn representations from data using a particular abstraction known as the computational graph. A computational graph is conceptually simple in that it represents the flow of data through the neural network’s layers as well as the operations that are performed at each layer.

Think of a computational graph as a step-by-step recipe or a flowchart for the neural network. Just like a recipe guides a chef through the cooking process, the computational graph guides the data through the neural network’s layers, showing what happens at each step and how the network transforms the data.

To you do all this, computational graph frameworks are used to implement these deep learning algorithms. One of those is PyTorch, which we’ll certainly look at it in upcoming posts.

Let’s Scale Up Our Understanding

So we know we have inputs that go into a model and produce results. There’s actually another component to this that makes a model-program different from a traditional program.

I say that because a model-program in this context is not like a traditional program that explicitly contains a set of rules. Instead, it’s a mathematical representation that captures the relationships between inputs and outputs in the data through a set of parameters. Those parameters are sometimes called weights.

The analogy of a “weight” is borrowed from its common meaning in everyday language, where weight refers to the heaviness of an object. The weights determine the impact of the input data on the output. Just like a heavier object exerts more influence in a physical scenario, higher weights signify greater importance for the corresponding input in terms of the output.

I mentioned that the computational graph represents the flow of data through the neural network’s layers and operations. This flow actually has what’s called a forward pass and a backward pass. The forward pass is just the input to results. But the backward pass is a way for those results to be used as the basis for updating the weights.

That notion of performance is critical to the idea of testing. But let’s also consider how this idea differs from a traditional program yet also how it’s kind of the same. In a traditional program, the process is typically this:

input → action → output

The output is determined solely by the programmed rules and logic. There’s no inherent feedback mechanism to assess how well the program executed, as the output is entirely deterministic based on the input and the pre-defined rules. However, in machine learning, the process is more akin to this:

input → action → output → performance assessment

The model’s output is not predefined by strict rules but is generated based on the learned patterns and representations from the data. After producing the output, the model’s performance is assessed by comparing its predictions to the actual outcomes. The assessment provides valuable feedback on how well the model is performing on the task at hand.

Granted, with a traditional program we can check if the implementation works as we believe it did. But there’s no inherent testing there. This is why we have test frameworks at various abstraction levels to help us look for observations or we just check for ourselves. But in a machine learning context, the very nature of assessment is built it. This doesn’t mean you don’t need humans looking at the output but it does mean humans have even less of an excuse for testing in this context.

More Scaling Up of Our Understanding

So far this is a little black box — or blue box, given the visuals — but now let’s shift slightly (but only slightly) into a more white box understanding.

Let’s reframe our inputs as observations. Observations are items or data points about which we want to predict something. In order to predict, I presumably have some target that I will use as the basis for my prediction. After all, I’m predicting something. The target is what that something actually is. We often give these targets labels and these labels correspond to an observation. Sometimes, these labels known as the ground truth.

The term “ground truth” emphasizes that these labels represent the true, correct values you expect to learn so that you can predict accurately.

Given this slight reframing, a model is a mathematical expression or a function that takes an observation and predicts the value of its target label.

Again, in the context of execution, the model can be thought of as a program. It’s a program that runs the particular function which is some mathematical computation. It might be an incredibly complicated computation but it is just a computation nonetheless. In this context, we do still have our parameters or weights.

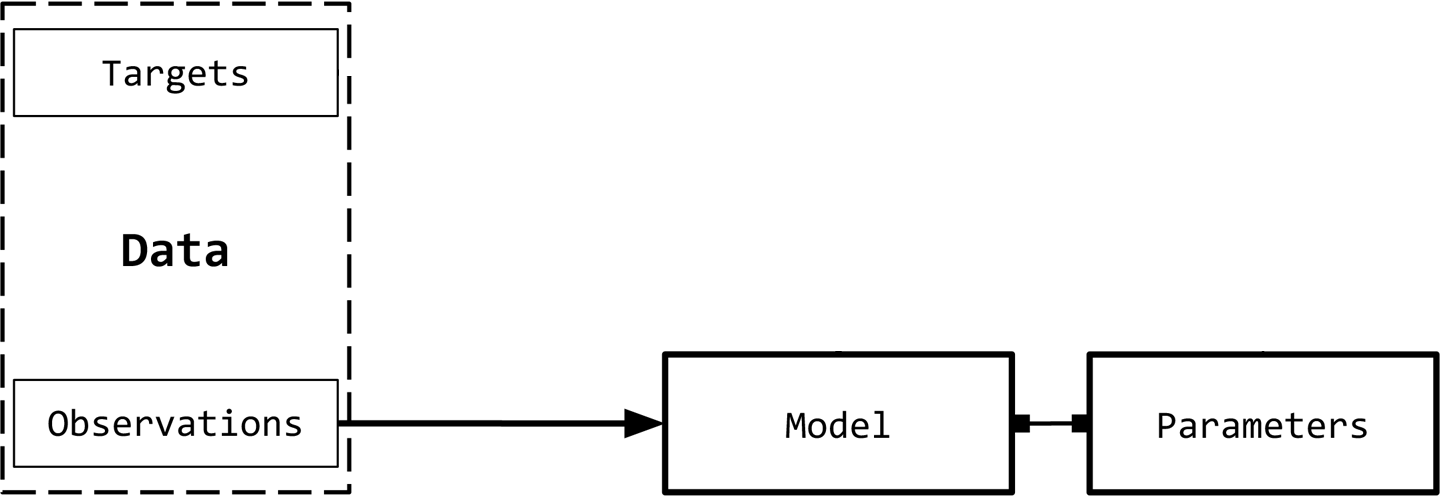
Given a target and its prediction, the loss function assigns a scalar real value that’s referred to, not too surprisingly, as the loss. A “real scalar value” just refers to a single numerical value that can be any real number on the number line. In the context of machine learning, it represents a continuous and unbounded quantity. The idea here is that the lower the value of the loss, the better the model is at predicting the target.

The Path to Supervised Learning

What this does is take us into supervised learning. In supervised learning, a model is trained using labeled data, meaning observations with corresponding targets. The loss function plays a critical role in guiding the learning process towards making accurate predictions on new, unseen data.

So now let’s bring our black (well, blue) and white boxes together.

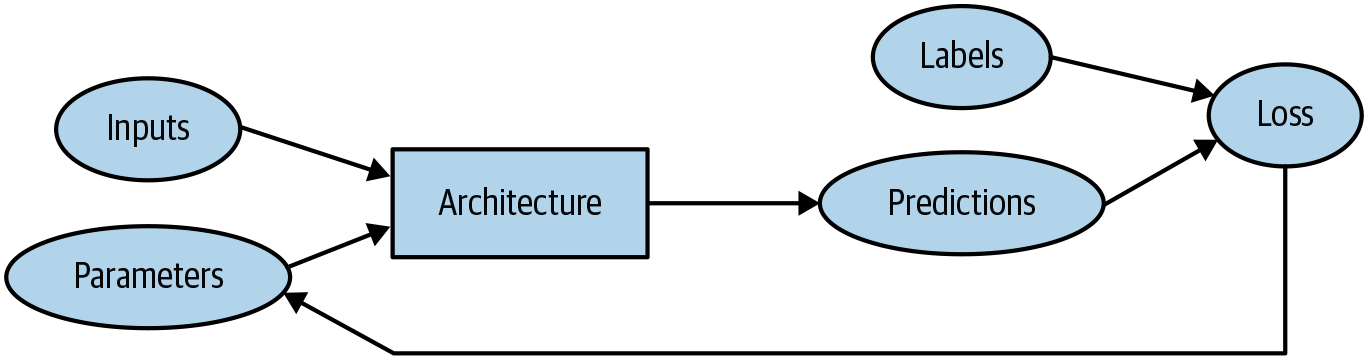
The specific functional form of a model is often called its architecture. When I say “functional form of a model” just understand that as the specific way that the model structured and how it processes input data to produce output predictions. It’s like the blueprint or design that defines how the model works and learns from data.

Thus the functional form in essence creates an experimental platform. And we run our experiments — our tests — on that platform. All good experiments have independent and dependent variables. In this context, the predictions are calculated from the independent variables, which is the data not including the targets. The targets (labels) are the dependent variables. The results of the model are called predictions. The measure of performance of model is called the loss. The loss depends not only on the predictions, but also on having the correct labels.

Notice how we have some structure to the data above, such as one dimensional arrays as well as a matrix.

What this shows us is that, given a dataset with some number of observations, we want to learn a function (a model) parameterized by weights.

But wait a minute! I thought we used models to do all this. Now you’re saying we have to learn the model. So do we use a model that we learn on the fly?

The term “model” refers to a conceptual representation of a mathematical function or algorithm that captures the relationships between inputs and outputs in a given problem domain. It’s a blueprint or framework that defines how the data should be processed to make predictions. When we talk about “learning a model,” we mean that we’re determining the specific values of the model’s parameters (such as those weights) that best fit the data in the given problem. These parameter values are adjusted during the training process, allowing the model to adapt and become effective at making predictions.

So we use the term “model” to represent the abstract concept of the mathematical relationship between inputs and outputs but when we “learn a model” we’re adjusting the model’s parameters to find the best fit for the data, making it a “learned instance” of that abstract concept.

Supervised learning is the process of finding the optimal parameters that will minimize the cumulative loss for all of the observations. The goal of supervised learning is thus to pick values of the parameters that minimize the loss function for a given dataset.

And what this tells us is that supervised learning is a form of computation that’s teaching a program to learn from examples. So imagine you have a bunch of examples, like pictures of animals. You also know what each animal is. You want the program to figure out how to recognize different animals correctly just like you can do. To do that, the program tries different approaches until it finds the best way to make accurate predictions.

This ‘best way’ involves adjusting certain settings, just like tuning a musical instrument, until it gets the answers as close as possible to what’s correct. And it knows what’s correct because we’ve told it what correct looks like; we’ve supervised the learning. The ultimate outcome here is to make the program really good at recognizing animals, so it can work well even with new pictures that it hasn’t seen before.

You can replace “pictures” above with “text” or “sounds” or “videos” and the same thing essentially applies.

There are also techniques known as unsupervised learning and reinforcement learning but those I’m leaving aside for now.

If you want to see a context where I talked about the basis of reinforcement learning, you can check out my Pacumen series.

Wrapping Up

So with all this said, consider again those statements from Weidman about what a neural network is:

• A neural network is a mathematical function that takes in inputs and produces outputs.
• A neural network is a computational graph through which multidimensional arrays flow.
• A neural network is a universal function approximator that can in theory represent the solution to any supervised learning problem.

We’ve now looked at what each of those mean conceptually. I hope you’ll agree that the concepts really aren’t all that difficult. And, as I showed above, the idea of testing is built right in. This doesn’t mean we don’t need humans to do testing. What it means is that there are plenty of hooks in place for quality and test specialists who want to critically engage with these concepts and with the technology.

A lot of thinking that goes into artificial intelligence is all about reasoning about how humans think. Specialist testers, at least so I argue, are good at understanding categories of error and the theory of error, both of which find ready application in how humans think. This is because humans can think fallaciously or make cognitive mistakes when they engage with complex things or apply biases that they are sometimes only dimly aware of.

Sometimes when you talk about this kind of stuff, someone might think you’re no longer talking about testing. But, in fact, I would argue you’re engaging with one of the most important parts of it.

Humans are building technology that will augment us in ways that have largely been unprecedented in our evolutionary history. Since we’re the ones building it, it’s safe to assume we’re building it with some of our flaws as well. So let’s start thinking about how to test it. In fact, we need to be long past the “thinking about how” stage and well into the “demonstrating how” stage.